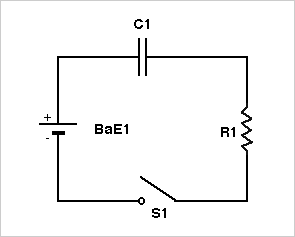
RC CIRCUIT: CHARGING
In the circuit shown below the switch S1 is closed at t = 0 and it is assumed that the initial charge on the capacitor is zero.  The charge, q, on the capacitor at time t is given by

    q = Vb*C1*(1 - exp(-t/(R1*C1)))

where Vb is the battery voltage.  Note the use of parentheses in the exponent to clearly establish that the product (R1*C1) is in the denominator of the exponent.  Also note, when t >> R1*C1,  q = Vb*C1.

Under the conditions stated above, the current through resistor R1 at time t is given by

    I = (Vb/R1)*exp(-t/(R1*C1))

If one desires to find the time required for the charge on the capacitor to build up to some percent of its value for very long times, Vb*C1, one can let

    q = (fraction)*(Vb*C1)

where "fraction" is a number between 0 and 1 to represent some percent of the final value of  charge for very long charging times.  For example, for charging to 30% of Vb*C1, "fraction"=0.3.