Projection equations are equations that indicate the relationship between the magnitude of a vector and its component along an axis.  For isntance, given the vector and coordinate system shown below:

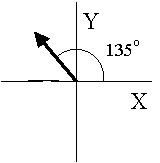
The projection equations are: where V is the magnitude of the vector, and V_x and V_y are its x- and y-components.  The orientation angle of this vecrtor is 135 degrees in a CCW direction with respect to the (right pointing) horizontal .

Here are general projection equations that apply even when the axes are rotated:

where qV is the angle of V counterclockwise with respect to the horizontal, and qx is the angle of rotation of the x-axis with respect to the horizontal.  For instance, suppose that V is  220 degrees from the horizontal and the x-axis is 27 degrees from the horizontal:

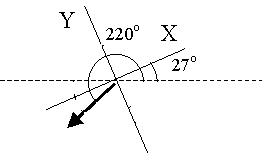
The projection equations are Although there are many simplifications of these equations that apply in special situations (e.g., when the axes are not rotated), if you always use these general versions then you will seldom make sign errors or trig errors.  The value of the orientation angle for vectors are known by Andes and never need to be typed in as numbers.