Loop Rule:  The sum of the potential changes around any closed path of a circuit must be zero.
 
            +/-V1 +/- V2 +/- V3 +/- … = 0    
 
In Andes the symbol for the potential change across a circuit element, like a resistor , a capacitor or a battery, is Vi.  Vi for each type of element is given by

        Resistor :  Vi = Ii*Ri       where Ii is the current through Ri
        Capacitor: Vi = qi/Ci       where qi is the charge on Ci
        Battery:     Vi = Vbi         where Vbi is the emf of the battery.     
        Inductor:   Vi = -L*dI/dt  (Note: In Andes dI/dt, the time rate of change of the current through the inductor, is written as dIdt.)


NOTE:  When the sum for use in the loop rule is constructed, the sign in front of each Vi term is determined by the "direction", which determines the sign of the changes in potential.  The convention for each circuit element is
(1) Potential change across a resistor is   -Vi , if the current is in the direction of sum, because this represents going from high to lower potential. It is +Vi otherwise.
(2)  Potential change across a capacitor  is -Vi, if the direction of the sum is from positive plate to negative plate,  because this represents going from high to lower potential.  It is +Vi otherwise.
(3)  Potential change across a battery is +Vi, if the direction of the sum is from negative plate to positive plate, because this represents going from low to higher potential.  It is -Vi otherwise.
(4) Potential across an inductor is +Vi, if the current is in the direction of the sum. It is -Vi otherwise. This differs from the treatment of resistors because the equation for voltage across an inductor is conventionally written with a negative sign in it (see above).


In each of these cases the direction of the sum is the direction that one is going around the closed loop to construct the loop rule sum.  See the examples below.
 
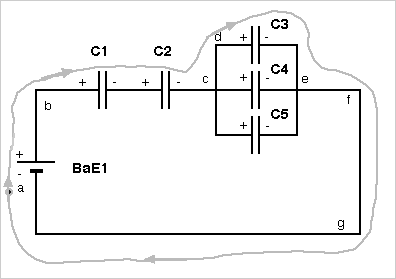
Capacitors example:  In the figure below, take the loop abcdefga and get
 
           Vb1 - V1 - V2 - V3 = 0  and use V1 = q1/C1, V2 = q2/C2 and V3 = q3/C3
 
Capacitor circuit
 
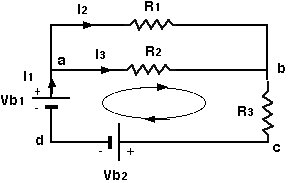
Resistors example: In the figure below, take the loop abcd and apply Kirchhoff's loop rule to get
 
           -V2 -V3 - Vb2 + Vb1 = 0 and use V2 = I3*R2 , V3 = I1*R3
          
Resistor circuit diagram