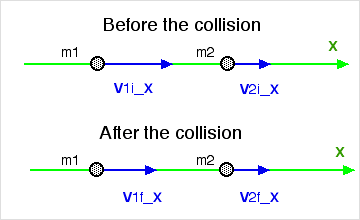
Consider an elastic collision between two masses, m1 and
m2, shown below, that is head-on
.
The term head-on
implies that the initial velocities of both particles lie along a
particular straight line. This condition simplifies the problem to a one
dimensional case where we will take the line of their common motion to
be the x axis.
Let p1ix, p2ix, p1fx and
p2fx be the x components of the linear momentum
of the two particles before and after the collision. Let
v1ix, v2ix, v1fx and
v2fx be the initial and final x components of
the velocity of the two masses before and after the collision.
Conservation of momentum yields
| (1) |
p1ix +
p2ix =
p1fx +
p2fx
|
Using the expression for linear momentum
| (2) |
m1*v1ix +
m2*v2ix =
m1*v1fx +
m2*v2fx
|
If the collision is an elastic collision, the total kinetic energy
before the collision is equal to the total kinetic energy after the
collision. This yields
| (3) |
K1i +
K2i =
K1f +
K2f
|
Using the expression for kinetic energy
| (4) |
0.5*m1*v1ix2 +
0.5*m2*v2ix2 =
0.5*m1*v1fx2 +
0.5*m2*v2fx2.
|
Equations (2) and (4) can be rearranged and factored as shown
below. By factoring both equations in the forms shown below and
dividing (4a) by (2) one gets two linear equations (2a) and (5) that
can be solved for the final velocities.
| (2a) |
m1*(v1ix-v1fx) = m2*(v2fx-v2ix) and
|
| (4a) |
m1*(v1ix-v1fx)*(v1ix+v1fx) = m2*(v2fx-v2ix)*(v2fx+v2ix)
|
Dividing (4a) by (2a) and re-arranging, one gets
| (5) |
v1fx - v2fx =
v2ix - v1ix
|
In other words, the relative velocity of the two objects after the
collision is equal to minus the relative velocity of the two objects
before the collision.
The two linear equations (2a) and (5) can be solved to get
| (6) |
v1fx = {(m1-m2)/(m1+m2)}*v1ix + {2*m2/(m1+m2)}*v2ix
|
| (7) |
v2fx = {(m2-m1)/(m1+m2)}*v2ix + {2*m1/(m1+m2)}*v1ix
|
Last modified: Tue Aug 15 22:34:20 EDT 2006