Homework: Roots of Nonlinear Equations

Due Friday, September 14, 2000 in class

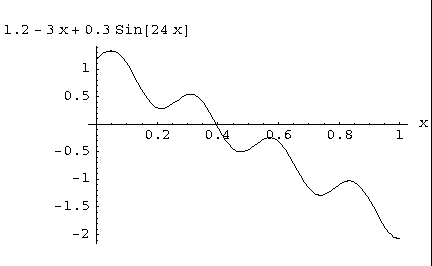
In this assignment, we will investigate the performance of several root finding routines acting on a number of test functions. We will examine the following test functions:

1. In my research, I must find the root of the following function on the interval [0, 1]:
   
2. Here is a polynomial on the interval [0, 1]:
   
3. This example is from solid state physics. This function describes the occupation of levels in a Fermi gas as a function of energy. The interval is [0,1].
   
4. An oscillating function on the interval [0,1]. Newton's method had better watch out!
   

1. In the file that will also contain your main program, write four subroutines containing the four test functions. First, I give the FORTRAN examples of the functions:
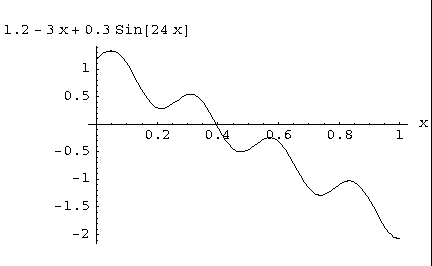
   1. pi = 3.1415926535897932D0
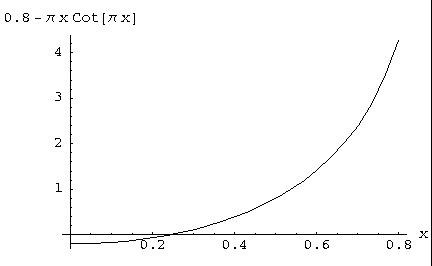
f1 = 0.8D0 - Pi*x/tan(Pi*x)
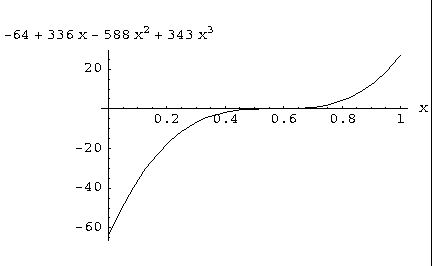
   2. f2 = -64 + 336*x - 588*x**2 + 343*x**3
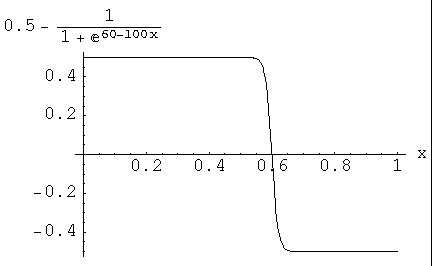
   3. f3 = 0.5D0 - 1.0D0/(1.0D0 + exp(60.0D0 - 100.0D0*x))
   4. f4 = 1.2D0 - 3.0D0*x + 0.3D0*sin(24.0D0*x)
   and then examples in C:
   1. pi = 3.1415926535897932;
return 0.8 - pi*x/tan(pi*x);
   2. return - 64 + 336*x - 588*pow(x,2) + 343*pow(x,3);
   3. return 0.5 - 1.0/(1.0 + exp(60.0 - 100.0*x));
   4. return 1.2 - 3.0*x + 0.3*sin(24.0*x);
   You should use double precision for all floating point variables and constants. In your main program, if you are using FORTRAN, you will have to declare the names of the four test functions to be EXTERNAL. In C, you will have to include prototypes of your four test functions at the beginning of the file. In order to use the various math functions in C, you will also have to include the math header file:

   #include <math.h>

   at the beginning of the file.
2. If you will be using Newton's method (see below), your subroutines will also have to return the first derivative. An example of how one might do this in FORTRAN is:

   C
   C  This function returns 0.5 - 1/(exp(60 - 100 x) + 1) and its derivative
   C
         double precision function f3(x,fprime)
         implicit none
         double precision x,fprime,temp
         temp =  exp(60.0D0 - 100.0D0*x)
   C
   C  This is the derivative of the function:
   C
         fprime = (-100.0D0*temp)/(1.0D0 + temp)**2
   C
   C  This is the function itself:
   C
         f3 = 0.5D0 - 1.0D0/(1.0D0 + temp)
         return
         end
    

   In C, the derivative fprime would be passed to the subroutine as a pointer.
3. For each of the four test functions, explain why it would --- or would not --- be difficult to find the root: Is the function approximately linear near the root? Is the function oscillatory?
4. Write a function that finds a root of a given function. Initial of students assigned to each method:
   • JO, MN, T-YC: Bisection Method
   • NG, SH, JM: Secant Method
   • JF, RM, JT: False-position Method
   • EW, HM: Newton's Method
5. Explain how your root-finding routine works. That is, start with a paragraph explaining, step by step, how the algorithm works. Then explain, step by step, the subroutine you wrote.
6. The root-finding routine should be saved in a file separate from your main program. It should have the following arguments:
   • The name of the function whose root is to be found.
   • The initial lower limit.
   • The initial upper limit.
   • The desired accuracy.
   If you are doing Newton's method, you only need to supply one initial value.
7. Using the ends of the interval as starting values, calculate the root of each of the four test functions to an accuracy of 5.0E-16. Print out your answer showing 16 digits past the decimal point. In Fortran, you do this by adding a format statement:

         write(*,11)y
    11   format('my results for f1=',F20.16)
   

   In C, you do this using:

     printf("my result for f1=%.16g\n",y);
   

   (I have no idea how you do this in C++.) Which cases converged?
8. If you are using Newton's method, you must specify one starting point. Use the left hand side of the interval as your starting point. If the routine does not converge using this starting point, try to find a starting value that does converge.
9. On the Internet, find a root-finding routine based on Brent's Algorithm. Use this routine to find the root for all your test functions. Is there agreement for the two methods in the cases that converged?
   • The FORTRAN version is often called zeroin.f and can be found in the GO (Golden Oldies) package; you will also need d1mach.f from the last assignment.
   • The C version is packed in a peculiar way; thus, I have provided a local copy: zeroin.c.
   • If you are using Newton's method, you do not have to download or use Brent's algorithm.
10. Let delta be the difference between the exact value for the root, determined above, and the value after n function calls. Plot log10(abs(delta)) as a function of the number of function calls n (log10 is logarithm base 10).
    • As discussed in class, one way to accomplish this would be to include a print statement of the form

            exactvalue = 3.14159265358979324D0
            print *,' log10(delta)=',log10(abs(x-exactvalue))
      

      in each of the four test function subroutines.
    • If you are using FORTRAN, your exactvalue should be a double precision variable. The D in the constant tells the compiler that the constant is a double precision number.
    • The domain of your plot should include n up to about 30 (that is, you should plot points for the first 30 steps).
    • Make a separate graph for each of the four test functions. Each graph should include a curve for the routine you wrote and a curve for Brent's Algorithm. You can do the graphs by hand on graph paper, if you prefer.
    You should be ready to explain these results.
11. You should be prepared to make a five minute presentation of your results to the class on the due date. If you will not attend this class, you must tell me as soon as possible.