Numerical Methods, MAT 350
Autumn 2001

Homework: Functional Minimization

Due Friday, September 28, 2000 in class.

The Traveling Salesman Problem

Here are some questions related to the Traveling Salesman problem. Have fun!
  1. A good introduction to this problem has been written by Stephan Mertens in Magdeburg, Germany. See TSP Algorithms in Action: Animated Examples of Heuristic Algorithms . List the strategies that are illustrated in the examples (with a one or two sentence explanation of each). To better see what is going is going in the examples, use the button.
  2. As mentioned in lecture, people tend to be quite good at solving optimization problems like the Traveling Salesman Problem. Try your skill with a version from Manu Konchady. There is no mention of the algorithm used, but it doesn't seem to be particularly good: occasionally I have been able to find a shorter route than the computer did. Record your result and the result found by the algorithm. Can you beat the computer?
  3. Visit a web page from Frankfurt that uses a simulated annealing approach. It seems that the Germans really like this sort of problem. Record the number of cities and the number of iterations before the path finally settled down. What was the temperature?
  4. Look at an approach using a genetic algorithm from Erlangen (where I used to live). Hit the button "quality-graph" to get a graph of the path length as a function of iteration. Start by pressing Continue. Unfortunately, there is no graphic that gives a picture of the path itself: just the path lengths are shown. The results are more interesting if you choose: Describe the meaning of "children" and "parents" in this algorithm. Explain briefly how the algorithm works. What happens when there is only one parent?
  5. A different approach, one which is more specific to the Traveling Salesman problem, is shown by Tanya Filipova at the Joint Institute for Nuclear Research, Dubna, Russia has an "Elastic Net Method" for the traveling salesman problem. Briefly explain this strategy.
    There is also a version at Regensburg (a city about 150km South-East of Erlangen).
  6. Another very trendy approach to this kind of problem is the Neural Net.
  7. The Traveling Salesman problem is an example of an "NP-hard" problem. Find the definition of "NP-hard." You can look somewhere on the internet; you can look in a book. It is easy to find a definition that is incomprehensible; try to find a definition that you can understand. Also, find another example -- other than the Travelling Salesman Problem -- of an "NP-hard" problem and briefly explain this example, and why it seems to be "NP-hard." Be sure to mention where you found your information.
  8. Finally, a head scratcher question: You may have noticed that, for any optimum solution of the Traveling Salesman problem, the path does not cross itself. Can you explain why this is so? Hint: consider two paths which are identical except for one "crossing."
    A path Another path

    Fitting Data to a Straight Line

    This is a short programming exercise which illustrates the minimization of a function for the purpose of fitting a curve. Consider the following data points (the numerical values are given below):
    plot of data points
    We would like find the line y=a+bx which minimizes the chi-square best fit function.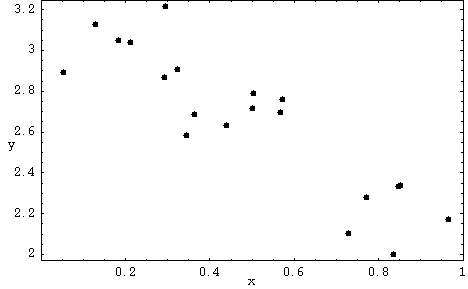
    1. Print out a copy of the above graph and try to make a best fit estimate by "eyeball" using a ruler and a pencil. Record your values you obtain for a and b using this procedure.
    2. Read the Section "Fitting Data to a Straight Line" in Chapter 15 of your text. For simplicity we will assume that the errors associated with the y values are all equal to 1.
    3. Now, close your textbook and derive the formulas for a and b in terms of the data points.
    4. Write a simple program (there is no need to use subroutines here) to calculate a and b.
      • In C, the data points are: 
        #define NPOINTS 20  /* This is the number of data points*/
/* Here is a vector containing the x-values */
float x[NPOINTS]={0.0516082, 0.128727, 0.183212, 0.210909, 0.290406,
0.294732, 0.321201, 0.344, 0.363073, 0.43772, 0.500713, 0.50225,
0.565908, 0.571533, 0.72712, 0.770354, 0.835032, 0.845504, 0.850564,
0.964372};
/* Here is a vector containing the y-values */
float y[NPOINTS]={2.89574, 3.12705, 3.05028, 3.03999, 2.86911,
3.21711, 2.91052, 2.58598, 2.68829, 2.63369, 2.71827, 2.79343,
2.69613, 2.75923, 2.10584, 2.2825, 1.99966, 2.33427, 2.3399, 2.17499};
      • In FORTRAN, we can use DATA statements to define the points: 
              INTEGER NPOINTS
      PARAMETER (NPOINTS=20)
      REAL X(NPOINTS), Y(NPOINTS)
C          Here is a vector containing the x-values 
      DATA X/0.0516082, 0.128727, 0.183212, 0.210909, 0.290406,
     & 0.294732, 0.321201, 0.344, 0.363073, 0.43772, 0.500713, 
     & 0.50225, 0.565908, 0.571533, 0.72712, 0.770354, 0.835032,
     & 0.845504, 0.850564, 0.964372/
C     Here is a vector containing the y-values
      DATA Y/2.89574, 3.12705, 3.05028, 3.03999, 2.86911, 3.21711,
     & 2.91052, 2.58598, 2.68829, 2.63369, 2.71827, 2.79343, 2.69613,
     & 2.75923, 2.10584, 2.2825, 1.99966, 2.33427, 2.3399, 2.17499/
        The DATA statements must come after all of the declarations and before any of the executable statements in a program.
      • Hint: use "copy" and "paste" to get the above lines into your program.
      • As always, your code should be well commented. In this case it is particularly useful to define the important variables.
    5. Compare the results of your computer program with the results you obtained by "eyeballing" the graph.

    Minimum of a function in one dimension

    I have a function y = f(x) which has a root in the interval (0,1). I would like to find that root to as great an accuracy as possible. Would I do better to find the root of f(x) directly or could I just as well find the minimum of f(x)² ? Explain why.